システムの信頼度は、製品やプロジェクトの成功に直結する重要な指標です。本記事では、信頼性工学の基本概念としてシステムの信頼度を取り上げ、その計算方法や実際の活用例について解説します。信頼性を高めるための対策を知ることで、システム全体のパフォーマンスを向上させる手法を学びましょう。
1. システム信頼度とは？
システム信頼度とは、システムが正常に機能し続ける確率のことです。通常、故障が発生しない限りシステムは信頼性を保ちますが、一定時間内に故障が発生する確率を理解することは、システムの運用計画やメンテナンスにおいて非常に重要です。
2. システム信頼度の計算方法
システム信頼度は、故障率を用いて計算され、次の式で表されます。
信頼度 = exp( – 故障率 × 時間 )
例: 故障率0.01のシステムが100時間稼働した場合は、約36.8%の信頼度です。
3. 具体例と問題
問題1: 故障率0.005、稼働200時間で信頼度は？
解答: 信頼度は約36.8%
問題2: 故障率0.002、稼働100時間で信頼度は？
解答: 信頼度は約81.9%
並列システムと直列システムの信頼度
システムって、実は「並列」と「直列」という2つのタイプがあるんです。これらの信頼度の計算方法が全然違うので、ぜひ覚えておいてくださいね。
直列システム
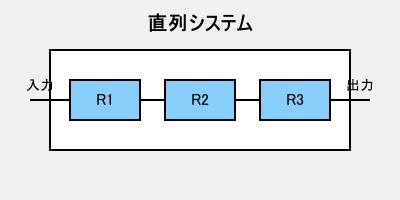
直列システムは小学校で習った電気回路を思い出してください。電球を1列に並べたやつです。1つでも切れたら、全部消えちゃいますよね。システムの信頼度も同じ考え方なんです。
直列システムの信頼度は、各コンポーネントの信頼度をかけ算して求めます。つまり：
R(直列) = R1 × R2 × R3 × … × Rn
例えば、3つのコンポーネントがあって、それぞれの信頼度が0.9、0.95、0.8だとしましょう。
R(直列) = 0.9 × 0.95 × 0.8 = 0.684 (68.4%)
信頼度が6割強というちょっと厳しい結果になりましたね。これが直列システムの弱点なんです。
並列システム
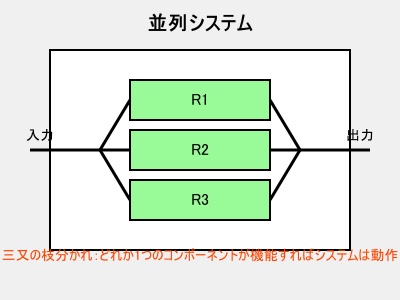
一方、並列システムは「どれか1つでも動いていればOK」というシステムです。例えば、非常用電源を2つ用意しておくようなイメージです。
並列システムの信頼度は、各コンポーネントが故障する確率を掛け算して、それを1から引くことで求められます。数式で書くと：
R(並列) = 1 – (1 – R1) × (1 – R2) × … × (1 – Rn)
さっきと同じ3つのコンポーネント（信頼度0.9、0.95、0.8）で計算してみましょう。
R(並列) = 1 – (1 – 0.9) × (1 – 0.95) × (1 – 0.8) = 0.999 (99.9%)
信頼度があがりましたね。これが並列システムの強みなんです。
実際の応用
実際のシステムでは、直列と並列が組み合わさっていることが多いんです。例えば、データセンターのサーバーシステムを考えてみましょう。
- 電源ユニット（並列：2つ）
- CPU（直列：1つ）
- メモリ（並列：4枚）
- ハードディスク（並列：2台）
こういう複雑なシステムの信頼度を計算するのは、ちょっと大変ですが、基本的な考え方は同じです。並列部分と直列部分をそれぞれ計算して、最後にまとめるんです。
まとめ
システムの信頼度を考えるとき、直列と並列の違いを理解するのはとても大切です。直列システムは1つでも故障すると全体が停止してしまうので、信頼度が低くなりがちです。一方、並列システムは冗長性があるので、高い信頼度を実現できます。
でも、並列システムにはコストがかかるので、バランスを考えながら設計するのが重要なんですよ。結局のところ、システム設計って「信頼性」と「コスト」のバランスをとるのが大事なんです。
コメント