“QC検定2級の試験では、回帰分析がほぼ毎回出題されます。出題パターンは多くないため、この分野をマスターすることで合格に大きく近づきます。
この記事では、相関分析と単回帰分析の完全攻略法を詳しく解説します。過去問の解説だけではわかりにくい点についても、わかりやすく説明します。”
- QC検定2級を受験予定の方
- 回帰分析や相関分析の理解を深めたい方
- 過去問の解説だけでは物足りない方
QC検定2級における相関係数と回帰分析の実施方法
- 相関係数や分散分析を実施し、データの直線的な関係を確認します。
- 単回帰式 $y=a+bx$を用いて、切片 $a$ と 傾き $b$ を算出します。
データに直線の関係が確認された後、その関係を数式で表す流れが一般的です。以下に、用語の説明と計算方法を詳しく解説します。中学校で習う一次関数の式 $y=ax+b$とは異なり、QC検定では $a$ が 切片、$b$ が 傾き ですので、その違いに注意してください。
相関係数の計算と確認方法
相関係数 $r$ は、2つの変数 $x$ と $y$ の直線的関係の強さを示します。
- 計算過程が複雑で、間違えやすいため注意が必要です。
- 相関係数 $r$ の値は -1 から 1 の範囲に収まります。
- 値がこの範囲外に出た場合は、計算ミスの可能性があります。
相関係数の計算方法
相関係数は、2つの変数がどれだけ直線的に関連しているかを示す指標です。計算式は以下の通りです:
$r=\frac{S_{xy}}{\sqrt{S_xS_y}}$
この式はQC検定2級でよく出題されるため、覚えておくことが重要です。
相関係数を計算するためには、以下の平方和を用いる必要があります。問題文で与えられることが多いですが、場合によっては表から値を読み取り、自分で計算する必要があります。公式は次の通りです:
$S_x=\sum{x_i^2}-\frac{(\sum{x_i})^2}{n}$
$S_y=\sum{y_i^2}-\frac{(\sum{y_i})^2}{n}$
$S_{xy}=\sum{x_iy_i}-\frac{(\sum{x_i})(\sum{y_i})}{n}$
平方和の計算は複雑になることがあるため、計算ミスに注意が必要です。一般的な業務用電卓での計算方法については、以下の記事で詳しく解説しています:
計算結果の相関係数 $r$ が 0.7 以上 の値を示す場合、$x$ と $y$ の間には強い直線的関係があると判断できます。相関係数以外の重要な指標についても、後ほど説明します。
単回帰式の説明
相関係数を計算して、$x$と$y$ の間に直線的な関係があることが確認できたら、次に 単回帰式 を用いてその関係を数式で表します。
単回帰式は以下の形で表されます:
$y=a+bx$
ここで係数$a$と$b$は最小二乗法を用いて以下のように推定します。計算式は次の通りです:
- 係数 $b$ は次の式で求められます:
$b=\frac{S_{xy}}{S_x}$
- 係数 $a$ は次の式で求められます:
$a=\bar{y}-b\bar{x}$
これらの係数を計算するだけでは、単回帰式の妥当性が確認できません。問題では、分散分析表 を作成し、式の妥当性を検討する流れが一般的です。分散分析表の作成方法については、変動の計算 とその意味について解説した後に触れます。
変動の分解
分散分析表を作成するためには、公式を覚えるだけでなく、基本的な概念を理解することが重要です。まず、データがどれだけ散らばっているかを示す 変動 を計算します。変動の関係は以下のイメージ図を参照してください。
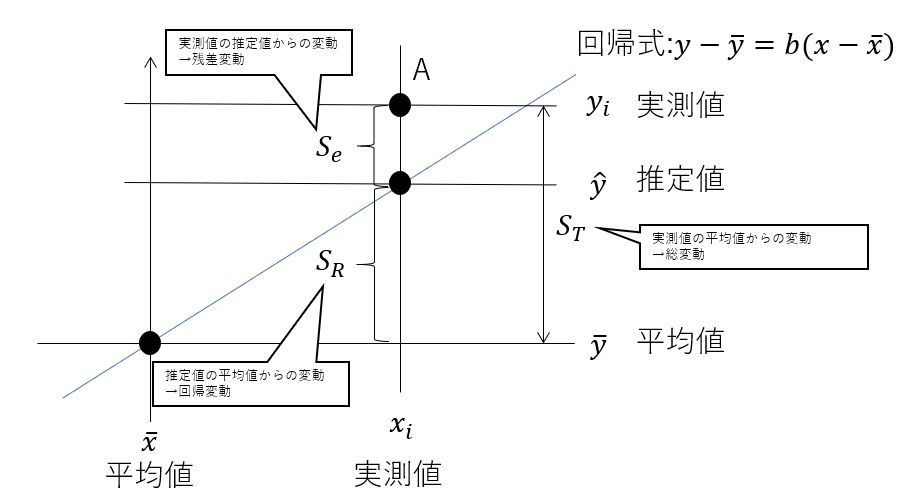
総変動は 残差変動 と 回帰変動 に分解できます。これにより、次のような関係が成り立ちます:
総変動$S_T=S_y$
回帰変動$S_R=\frac{S_{xy}^2}{S_x}$
残差変動$S_e=S_T-S_R$
イメージ図を見ると、回帰変動 $S_R$ と残差変動 $S_e$ を比較できます。$S_e$ が十分に小さい場合、回帰式の推定が妥当であると判断できます。
回帰式の妥当性を判断するためには、次の比率を確認します:
$\frac{回帰式による変動S_R}{回帰式からの誤差による変動S_e}$
この比率が一定以上であれば、回帰式は妥当とされます。実際には、不偏分散 $V_R$ と $V_e$ の比率を計算して、スケールを揃えた比較を行います。
分散分析の実施方法
分散分析を行うために、まず帰無仮説 と 対立仮説 を設定します。
- 帰無仮説: $b = 0$(回帰直線の傾きが0である)
- 対立仮説: $b \neq 0$(回帰直線の傾きが0ではない)
次に、分散分析表を作成します。この表は、F値を求めて検定を行うことが目的です。分散分析表の作成自体も試験で得点に結びつく可能性があるため、正確に作成することが重要です。
| 平方和 | 自由度 | 不偏分散 | F値 | |
| 回帰変動 | $S_R=\frac{S_{xy}^2}{S_x}$ | $\phi_R=1$ | $V_R=\frac{S_R}{\phi_R}$ | $F=\frac{V_R}{V_e}$ |
| 残差変動 | $S_e=S_T-S_R$ | $\phi_e=n-2$ | $V_e=\frac{S_e}{\phi_e}$ | |
| 総変動 | $S_T=S_y$ | $n-1$ |
F値を計算した後、棄却限界値 を調べます。F表 から棄却限界値 $F(\phi_R,\phi_e)$ を読み取り、計算したF値と比較します。F値が棄却限界値を上回る場合、対立仮説を採択し、回帰直線が妥当であると判断します。
試験では、相関関係がある問題が多く出題される傾向があります。相関がない場合、後続の問題に影響を与えるためです。
まとめ
QC検定2級の試験では、相関分析 と 回帰分析 が重点的に出題されます。これらの分野は出題パターンが少なく、攻略しやすいです。
- 相関分析 では、相関係数の算出がよく問われます。平方和 の計算と合わせて、しっかりと習得しておくことが重要です。
- 回帰分析 では、2変数間の直線性を検定し、回帰直線 を推定する流れが一般的です。分散分析表 を覚えておけば、こちらも対応しやすいです。
試験対策に役立つ詳細な情報については、以下の記事をご覧ください:





コメント