QC検定2級の実験計画法は、毎回出題される重要な分野です。計算が複雑で難しく感じるかもしれませんが、問題のパターンは少なく、ポイントを押さえれば高得点を狙えます。このガイドを活用して、効率的に得点を伸ばしましょう。
記事に記載の公式は全て事前に確認していますが、万一間違いを発見された場合はお知らせください。
QC検定2級 実験計画法のステップ別解答ガイド
実験計画法の問題は、以下のステップに従って分散分析が進行します。
- 帰無仮説と対立仮説を立てる(試験ではすでに用意されていることが多いです)。帰無仮説は「変化がない」という仮定で、対立仮説は「変化がある」という仮定です。
- 分散分析表の計算(各要因の影響を測定するために、平方和や自由度を計算します)。
- 平方和の計算(各データ点と平均値の差を二乗して合計する計算です)。
- 自由度の計算(データの自由な変動を表す値で、サンプルサイズや要因の数に基づいて計算します)。
- 分散分析表の穴埋め(計算結果を基に、分散分析表の各項目を埋めていきます)。
- 棄却限界値をF表から読み取り、分散比と比較して検定する(棄却限界値は仮説を棄却するための基準で、分散比と比較して判断します)。
分散分析についての説明
具体的な公式に入る前に、まず分散分析の基本的な考え方を理解しておきましょう。
分散分析の目的は、因子(影響を与える要因)が特性値(観察される結果)にどの程度影響を与えているかを判定することです。
これから、実際の業務での具体例を使って、分散分析の応用方法を詳しく解説していきます。
QC検定2級 分散分析の具体的な応用例
分散分析は私の業務でも使用しています。たとえば、接着剤の種類による接着強度の差を調べる際に活用しました。具体的には、3種類の接着剤を使って、それぞれの接着強度に差があるかを分散分析で検証しました。
この場合、変化を加える要素が因子(今回は接着剤の種類)、そして観察する値が特性値(今回は接着強度)です。それぞれの接着剤をA1, A2, A3と設定し、繰り返し実験を行いました。(水準=接着剤の種類が3つ)
実験データがそろったら、平方和を計算し、その結果をもとに分散分析表の各項目を埋めていきます。
QC検定2級 分散分析の基本: 特性値の分解とその重要性
分散分析を行わなくても、単純に各水準の平均値を比較すればよいのでは?と思われるかもしれません。確かに、そうすることもあります。
しかし、その方法では偶然の誤差によって生じた差なのか、接着剤の種類を変えたことによる差なのかを客観的に判断することができません。
そこで、分散分析が必要になります。個々の特性値は下記のように分解できます。
$x_{ij}$=全データの平均値$\mu$+因子$A_i$による効果(変動)$\alpha_i$+誤差$\varepsilon_{ij}$
下図で図解しています。
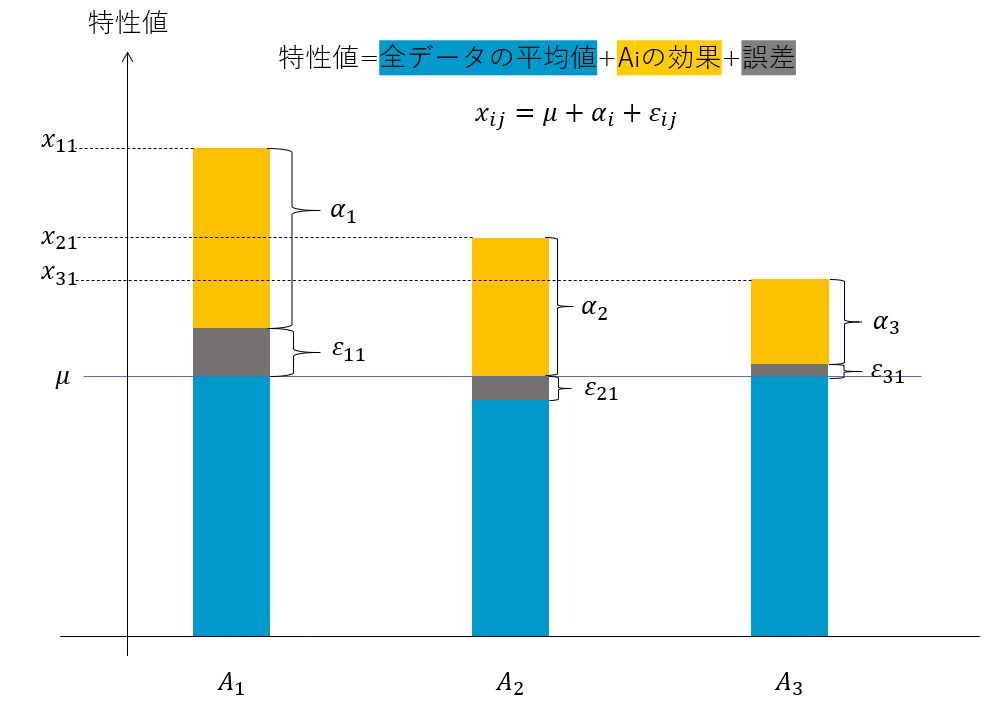
図では、「誤差のばらつき」と「接着剤の効果のばらつき」を比較し、接着剤を変えた効果を検証します。灰色の部分が「誤差のばらつき」、黄色の部分が「接着剤の効果のばらつき」を示しています。
- 水灰色の部分の幅に対応するのが$V_e$
- 黄色の部分の幅に対応するのが$V_A$
計算方法としては、$\frac{Aの効果による接着強度のばらつきV_A}{誤差のばらつきV_e}$を計算して、それがある値以上であれば、Aの効果があると判断します。
QC検定2級 実験計画法: 分散分析表の計算手順と公式まとめ
QC検定2級でよく出題される分散分析の問題には、次の3つの種類があります。
- 一元配置分散分析
- 二元配置分散分析
- 繰り返しのある二元配置分散分析
これらの各分析手法について、具体的な計算方法を確認し、試験本番で役立つ公式を簡潔にまとめて解説します。していきます。試験本番向けに公式をまとめています。
一元配置分散分析
1つの因子が特性値に対して効果があるかどうかを検定します。
例 接着剤の種類を変えたときの接着強度への影響を評価する。
計算は単純ですが、各水準の繰り返し数が違うパターンが出題されることがあります。平方和は$S_A$,$S_e$,$S_T$の3種類を計算する。自由度の計算方法は分散分析表の中に記載しています。
平方和の計算方法
修正項(correction term) $CT=\frac{ (全データの合計)^2}{全データ数}$
$S_T=\sum各データ^2-CT$
$S_A=\sum_{i}^{m}\frac{A_iデータの合計^2}{A_iのデータ数}-CT$
Aの水準数はmとする。
$S_e=S_T-S_A$
一元配置分散分析の分散分析表
| 平方和 | 自由度 | 不偏分散 | 分散比 | |
| 因子A | $S_A$ | $\phi_A=Aの水準数-1$ | $V_A=\frac{S_A}{\phi_A}$ | $F=\frac{V_A}{V_e}$ |
| 誤差e | $S_e$ | $\phi_e=\phi_T-\phi_A$ | $V_e=\frac{S_e}{\phi_e}$ | |
| 全体T | $S_T$ | $\phi_T=全データ数-1$ |
二元配置分散分析
2つの因子が特性値に対して効果があるかどうかを検定します。
例 A:接着剤の種類とB:つける材質を変更したときの接着強度への影響を評価する。
平方和$S_A$,$S_B$,$S_e$,$S_T$の4種類を計算する必要があります。自由度の計算方法は分散分析表の中に記載しています。
平方和の計算方法
修正項(correction term) $CT=\frac{ (全データの合計)^2}{全データ数}$
$S_T=\sum各データ^2-CT$
$S_A=\sum_{i}^{m}\frac{A_iデータの合計^2}{A_iのデータ数}-CT$
Aの水準数はmとする。
$S_B=\sum_{j}^{n}\frac{B_jデータの合計^2}{B_jのデータ数}-CT$
Bの水準数はnとする。
$S_e=S_T-S_A-S_B$
| 平方和 | 自由度 | 不偏分散 | 分散比 | |
| 因子A | $S_A$ | $\phi_A=Aの水準数-1$ | $V_A=\frac{S_A}{\phi_A}$ | $F=\frac{V_A}{V_e}$ |
| 因子B | $S_ B$ | $\phi_B=Bの水準数-1$ | $V_B=\frac{S_B}{\phi_B}$ | $F=\frac{V_A}{V_e}$ |
| 誤差e | $S_e$ | $\phi_e=\phi_T-\phi_A-\phi_B$ | $V_e=\frac{S_e}{\phi_e}$ | |
| 全体T | $S_T$ | $\phi_T=全データ数-1$ |
繰り返しのある二元配置分散分析
2つの因子の効果+2つの因子が組み合わさった交互作用の影響があるかどうかを検定したいときに使います。
例 A接着剤の種類とB相手の材質を変更したときの接着強度への影響を評価し、かつ接着剤の種類と材質の組み合わせA×Bの効果も評価したい。
平方和は$S_A$,$S_B$,$S_{AB}$,$S_{A×B}$,$S_e$,$S_T$の6種類を計算する必要があります。計算量がとにかく多く暗記する式も多いです。特にA×Bの平方和$S_{A×B}$は直接算出することができません。
一度AとBの効果をまとめた平方和$S_AB$を計算してそこからA単体の効果による変動$S_A$,B単体の効果による変動$S_B$を引くことによって求めます。
繰り返しのある二元配置分散はよく出てくるので、押さえておきたい問題になります。
自由度の計算方法は分散分析表の中に記載しています。
平方和の計算方法
修正項(correction term) $CT=\frac{ (全データの合計)^2}{全データ数}$
$S_T=\sum各データ^2-CT$
$S_A=\sum_{i}^{m}\frac{A_iデータの合計^2}{A_iのデータ数}-CT$
Aの水準数はmとする。
$S_B=\sum_{j}^{n}\frac{B_jデータの合計^2}{B_jのデータ数}-CT$
Bの水準数はnとする。
$S_{AB}=\sum\frac{(A_i B_jのデータの合計)^2}{繰り返し数}-CT$
$S_{A×B}=S_{AB}-S_A-S_B$
$S_e=S_T-S_A-S_B-S_{A×B}$
| 平方和 | 自由度 | 不偏分散 | 分散比 | |
| 因子A | $S_A$ | $\phi_A=Aの水準数-1$ | $V_A=\frac{S_A}{\phi_A}$ | $F=\frac{V_A}{V_e}$ |
| 因子B | $S_ B$ | $\phi_B=Bの水準数-1$ | $V_B=\frac{S_B}{\phi_B}$ | $F=\frac{V_A}{V_e}$ |
| 交互作用A×B | $S_ {A×B}$ | $\phi_{A×B}=\phi_A×\phi_B$ | $V_{A×B}=\frac{S_{A×B}}{\phi_{A×B}}$ | $F=\frac{V_{A×B}}{V_e}$ |
| 誤差e | $S_e$ | $\phi_e=\phi_T-\phi_A-\phi_B-\phi_{A×B}$ | $V_e=\frac{S_e}{\phi_e}$ | |
| 全体T | $S_T$ | $\phi_T=全データ数-1$ |
棄却限界値をF表から読み取り効果の有無を判定する
分散比が計算できたら、F検定を行うために、F表という表から棄却限界値を読み取る必要があります。
実務の現場ではエクセルにデータを打ち込めば分散分析表の作成も検定も自動でやってくれるのですが、試験では自分で表を見て読み取らなければなりません。
棄却限界値の表は試験問題に添付されています。分散比の分子と分母の自由度を逆に表を見てしまわないように気を付けましょう。F表は5%と1%の有意の値が上下並んで書かれていることが多いです。
棄却限界値は$F(分子の自由度,分母の自由度,0.05)$のように表されます。
下記に読み取りの例を示しています。下の例では$F(\phi_A,\phi_e,0.05)=19$なので,分散値を19と比較して大きければ有意差あり、小さければ有意差なしと判断します。
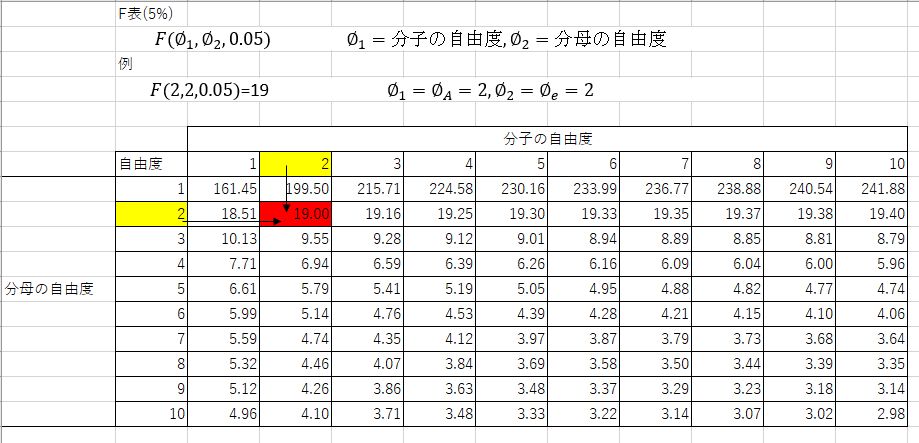
ここまでが一連の流れになります。
最大の関門は平方和の計算です。時間と戦いながら、大量の計算をする必要があります。
大量の計算を短時間でこなすためのおすすめの電卓と使い方については下記の記事で解説しています。
まとめ
いかがでしたでしょうか。実験計画法の分野は計算が複雑なことがわかると思います。しかし、QC検定2級では毎回、実験計画法の分野が出題され、一定の配点があります。
分散分析を使えば、ある因子を変化させたときに効果があるのかを判定できます。試験対策として平方和の計算方法と分散分析表をまとめました。
過去問の傾向を踏まえた対策は以下の記事にまとめています。ご覧ください。





コメント