QC検定2級・3級の計算問題で悩んでいる方必見!この記事では、初心者がつまずきやすい計算問題の落とし穴を徹底解説し、得点力アップに役立つ練習問題も多数ご用意しました。以下の方に特におすすめです。
- 計算問題が難しいと感じている方
- テキストや過去問で計算ミスが多い方
- 高校数学まではクリアできたが、統計学に不安がある方
- 実践分野で得点できるが、手法分野で伸び悩んでいる方
- 3級に合格し、2級受験を考えている方
これらに該当する方は、ぜひこの記事を活用して得点力をアップさせ、合格を勝ち取りましょう!
【確率】二項分布とポアソン分布の計算
二項分布とポアソン分布は、初めて見ると難しそうに感じるかもしれませんが、実は2級レベルではシンプルな代入と足し算の繰り返しです。2級では積分などの難しい計算は出題されないので、心配はいりません。
| 分布の種類 | 確率$P_x$ | x期待値 | x分散 |
| 二項分布 | $P_x={}_n C_xp^x(1-p)^{n-x}$ | $np$ | $np(1-p)$ |
| ポアソン分布 | $P_x=e^{-\lambda}\frac{\lambda^x}{x!}$ | $\lambda$ | $\lambda$ |
- $n$:サンプル数
- $p$:故障率
- $x$:不適合品の数
- $\lambda=np$
高校数学の範囲からおさらいします。Cはコンビネーション(組み合わせ)の頭文字のCです。
例えば、${}_3 C_1$は3つの相異なるものの中から1つのものを選ぶ場合が何通りあるかを計算する時の記号です。答えは3通りですね。
また、ポアソン分布の中に出てくる!マークは階乗といって一個ずつ数字を小さくしながらかけていく記号です。具体例は以下の問題ででてきます。
【QC検定3級】組み合わせの場合の数の計算
解答
${}_5 C_2=\frac{5×4}{2×1}=10$
$6!=6×5×4×3×2×1=720$
基本的な計算を振り返ったところで確率の計算に入っていきましょう
解答
C(コンビネーション)を使う方法
二項分布の式$P_x={}_n C_xp^x(1-p)^{n-x}$に$n=4,x=1,p=0.1$を代入します。
${}_4 C_1×0.1×(1-0.1)^3=4×0.1×0.9^3=0.2916$
C(コンビネーション)を使わない方法
取り出した4つのサンプルを(A,B,C,D)とする。シリアル番号などで4つのサンプルは識別できるものとする。
サンプルに不適合品が含まれる場合の数は
$(A,B,C,D)=(×,〇,〇,〇)(〇,×,〇,〇)(〇,〇,×,〇)(〇,〇,〇,×)$の4通りである。
各場合について確率を計算し合計する。
$(×,〇,〇,〇)=0.1×(1-0.1)×(1-0.1)×(1-0.1)$
$(〇,×,〇,〇)=(1-0.1)×0.1×(1-0.1)×(1-0.1)$
$(〇,〇,×,〇)=(1-0.1)×(1-0.1)×0.1×(1-0.1)$
$(〇,〇,〇,×)=(1-0.1)×(1-0.1)×(1-0.1)×0.1$
$4通りの合計=4×0.1×0.9^3=0.2916$
計算過程も含めて二項分布で求めた確率と同じ値になっているのが分かります。ただし、サンプル数nが増えるとこのやり方で1つずつ列挙するのが難しくなります。例えば${}_5 C_2=10$通りだと抜け漏れなく列挙するのは難しくなります。

結果的に計算結果は同じなので二項分布の式を覚えて使いこなす方が圧倒的に楽に解けます。
【QC検定2級レベル】二項分布の範囲のある確率(不適合品が~個以下である)
2級レベルではC(コンビネーション)を使うのを前提として、各場合の足し算が加わってきます。
解答
不適合品が$x$個含まれる確率を$P(x)$と表すと、不適合品が1個以下である確率$P(x\leqq1)$は以下の2つの場合の足し算になります。
- 不適合品が0個である確率$P(x=0)={}_4 C_0×0.1^0×(1-0.1)^4=0.6561$
- 不適合品が1個である確率$P(x=1)={}_4 C_1×0.1^1×(1-0.1)^3=0.2916$
$P(x\leqq1)=P(x=0)+P(x=1)=0.9477$

不適合品が1つも含まれない確率を忘れないようにしましょう。
【QC検定2級レベル】ポアソン分布の範囲のある確率(不適合品が~個以下である)
不適合品が$x$個含まれる確率を$P(x)$と表すと、不適合品が1個以下である確率$P(x\leqq1)$は以下の2つの場合の足し算になります。
- 不適合品が0個である確率$P(x=0)=e^{-\lambda}\frac{\lambda^0}{0!}=0.6065$
- 不適合品が1個である確率$P(x=1)=e^{-\lambda}\frac{\lambda^1}{1!}=0.3032$
$P(x\leqq1)=P(x=0)+P(x=1)=0.9097$

不適合品が1つも含まれない確率を忘れないようにしましょう。
【統計検定】標本分散と不偏分散の違い
標本分散と不偏分散の違いもよく選択肢ででてきます。
この二つの間には分母の数字がサンプル数nか自由度n-1かという違いがあります。
試験本番では「不偏分散は分母はnだっけn-1だっけ」と暗記したはずでも迷います。
| 式 | 使い分け | |
| 標本分散 | $V=\frac{\sum{(x-\bar{x})^2}}{n}$ | サンプル数が十分多く正規分布と近似できるときに使う。 |
| 不偏分散 | $V=\frac{\sum{(x-\bar{x})^2}}{n-1}=\frac{S}{n-1}$ | サンプル数が少ない場合に母分散を推定するときに使う。 |
- $x$:サンプルデータの値
- $n$:データ数
- $S$:平方和$S=\sum{x^2}-\frac{(\sum{x})^2}{n}$
標本分散は取り出してきたサンプル数が十分に多いとき(n>300)に使用し、サンプルの分布が母集団の分布とほぼ同じとみなせるときに使います。
対して、不偏分散は取り出してきたサンプル数が少ない場合にあくまで母集団の分散の推定値として使います。偏りのない推定値なので不偏分散です。
QC検定で問題に出てくるデータは試験時間内に計算が終わる必要があるため、サンプル数少ないものが多いです(5個~10個)。なので、結果的に標本分散ではなく、不偏分散を計算する問題が多くなります。
【QC検定3級レベル】データから基本統計量を求める
解答
平均値$\bar{x}=\frac{\sum{x}}{n}=\frac{15.56+15.45+15.61+15.52+15.46}{5}=15.52$
平方和$S=\sum{x^2}-\frac{(\sum{x})^2}{n}=15.56^2+15.45^2+15.61^2+15.52^2+15.46^2$
$-\frac{(15.56+15.45+15.61+15.52+15.46)^2}{5}=0.0182$
標準偏差$\sigma=\sqrt{\frac{S}{n-1}}=\sqrt{\frac{0.0182}{4}}=0.0675$
ここでいう標準偏差とは不偏分散にルートを付けた数値です。
真に知りたい値の母集団の母分散はたった5つのサンプリングではわかりません。なのでサンプルから母分散の推定値である不偏分散を計算してルートを付けます。不偏分散の分母はデータ数n-1です。

同じ標準偏差でも
- 標本分散をサンプル数で割る標準偏差
- 不偏分散を自由度でわる標準偏差
の2種類があります。混同しないようにしましょう。
【QC検定2級レベル】t検定の推定検定量
解答
(1)■=5
検定推定量tでは不偏分散Vをサンプル数nで割ります。データの平均値$\bar{x}$は標準偏差$\sqrt{\frac{\sigma^2}{n}}$で分布するのですが、母分散$\sigma^2$はわからないので不偏分散Vを代わりに使っているわけです。
(2)◆=4
先ほどの問題にもでてきましたが、平方和を自由度n-1で割ると不偏分散Vになります。

不偏分散の分母にあたるのか、検定推定量の式の一部なのかを見極めましょう。
【統計検定】棄却限界値の選択
棄却限界値の選択問題はよく出てきます。なぜかというと同じ有意水準でも片側検定か両側検定かで棄却域が変わるうえ、自由度の組み合わせで選択肢を作りやすいからです。
【QC検定2級レベル】t検定の棄却限界値
解答
まず自由度は5-1=4なので①③⑤に絞れます。
両側検定か片側検定かは問題で示されている場合と自分で選択する場合があります。例えば
- 帰無仮説$H_0=\delta=0$
- 対立仮説$H_1=\delta\ne0$
であれば、$\delta$がプラス側に振れてもマイナス側に振れても差があることに変わりありません。この時は両側検定であることが分かります。
他には試験問題には後ろのページに以下のように検定の棄却域が図示されていることが多いです。
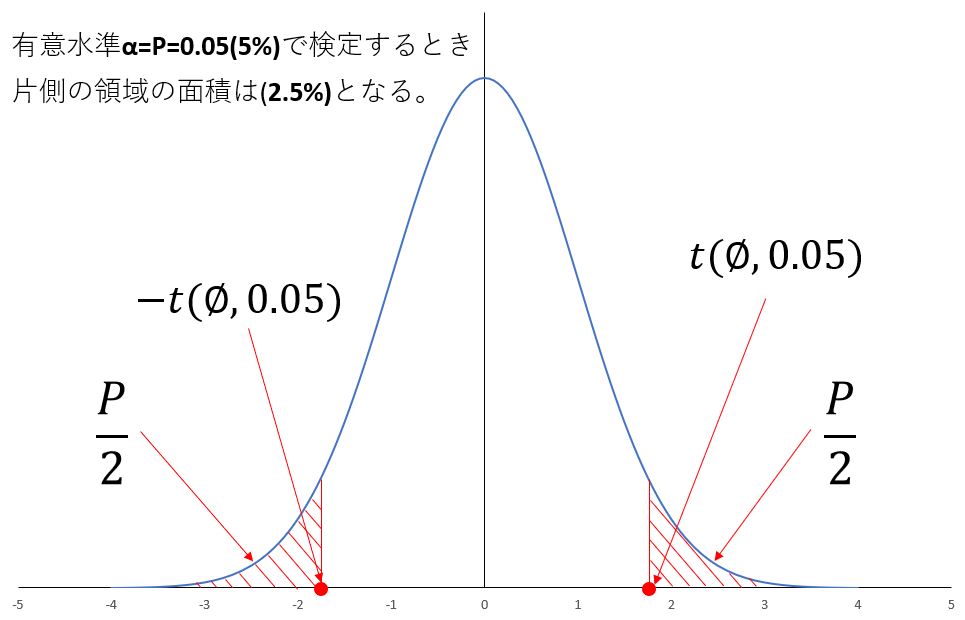
例えば①±t(4,0.025)だと両側の棄却域の面積を足して0.025なので有意水準2.5%の検定になります。⑤±t(4,0.10)だと両側を足して10%なので有意水準10%になります。
正解は③±t(4,0.05)になります。

単体で見ると難しくはないのですが、試験中に焦ると「あれ、どうだったかな」となることがあります。
まとめ
QC検定2級3級で頻出の内容で間違いやすい計算問題について解説しました。確率や検定は頻出ですが、問題のパターンが多く完答のハードルが高いです。過去問の傾向を踏まえたQC検定攻略法を解説しています。ぜひご覧ください。




コメント