QC検定2級・3級の合格を目指す皆さん、正規分布の問題は避けて通れません。本記事では、正規分布の基礎から応用までをわかりやすく解説し、練習問題もご用意しました。今すぐこの記事を活用して、確実に得点力をアップさせ、合格を勝ち取りましょう!
QC検定でつまづきやすい計算問題は以下の記事で解説しています。
正規分布とは?
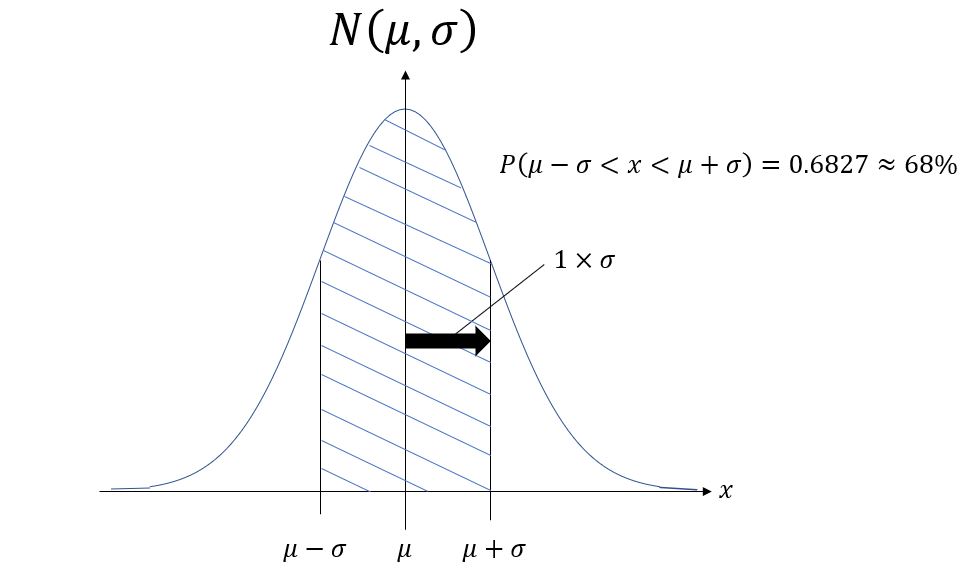
QC検定2級・3級で出題される正規分布の特徴を簡潔にまとめます。
- 正規分布は左右対称の釣り鐘型をしています。
- この形状は、分散 $V$($=\sigma^2$) によって決まり、分布がどの程度広がるかを示します。
- 常に一つの山(ピーク)を持ち、分散や平均が変わっても山が二つになることはありません。
- 平均が0、分散が1の正規分布を$N(0,1) $ と表し、これを標準正規分布と呼びます。
- 標準正規分布は、計算問題で頻繁に使用される基礎的な概念です。
正規分布の式は$f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp(-\frac{(x-\mu)^2}{2\sigma^2})$になります。
この数式はQC検定3級ではほとんど試験に出題されませんが、2級では理解が必要です。試験で重要なのは、この式自体ではなく、後で紹介する「変数変換」の計算方法です。
標準偏差$\sigma$の範囲と確率の関係
よく問われるのは、$1\sigma,2\sigma,3\sigma$の範囲が正規分布上で何%の確率を占めるのかです。まとめると以下のようになります。
$P(\mu-1\sigma<x<\mu+1\sigma)=68.3$%
$P(\mu-2\sigma<x<\mu+2\sigma)=95.5$%
$P(\mu-3\sigma<x<\mu+3\sigma)=99.7$%
($P(\mu-4\sigma<x<\mu+4\sigma)=99.9936$)%
ではこの情報をどうやって使うのかを練習問題で確認していきましょう。
$\sigma$の範囲練習問題
解答
規格内に収まっている製品の個数を求めて、全部の個数10000個から引く。
$10000×P(\mu-1\sigma<x<\mu+1\sigma)=10000×68.3%=6830$
$10000-6830=3170$個
$10000×P(\mu-2\sigma<x<\mu+2\sigma)=10000×95.5%=9550$
$10000-9550=450$個
$10000×P(\mu-3\sigma<x<\mu+3\sigma)=10000×99.7%=9970$
$10000-9970=30$個

工程では目標値に対して3シグマの範囲で管理するとか言います。この場合は10000個製品を作っても不適合品が30個以内になるように管理するという意味です。
変数変換を用いた正規分布の計算問題
常に求めたいのが定数×標準偏差$\sigma$の範囲であるとは限りません。例えば、寸法が**mm以下である確率や、重さが**g以上である確率とか標準偏差の値に関係なく規格値が決められていることの方が多いです。
試験問題に添付されているのは$N(0,1)$の場合の標準正規分布の表のみなので、問題で与えられた規格値の数字を$\frac{x-\mu}{\sigma}$で変換する必要があります。それでは練習問題をみてみましょう。
問1解答
3級で出る問題はパターンが決まっているので2ステップで解くことができます。問2問3も同じ流れでとけます。
ステップ1 変数変換
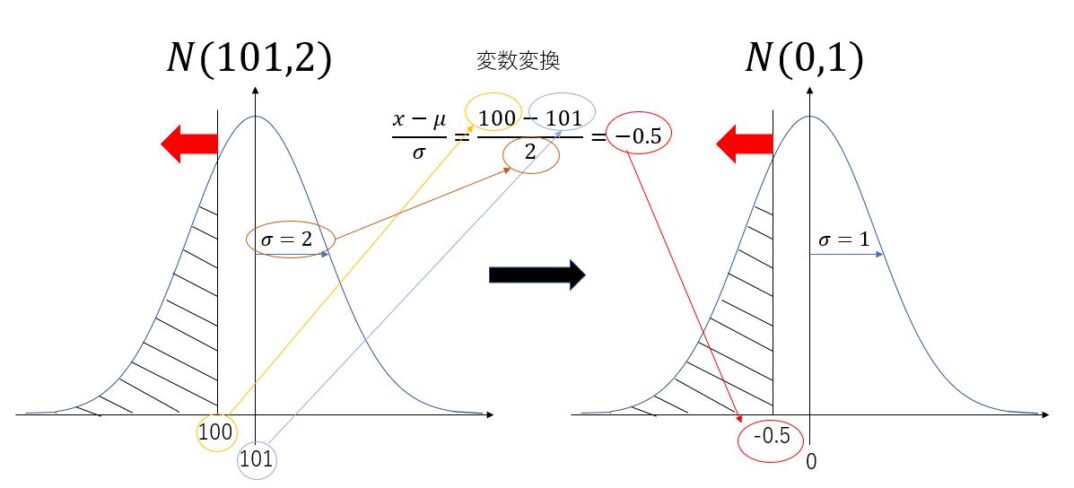
板の長さ寸法を$x$と置くと
$\frac{x-\mu}{\sigma}=\frac{100-101}{2}=-0.5$
ステップ2 標準正規分布表の読み取り
変数変換で100mm以下は標準正規分布上で-0.5以下と変換されました。標準正規分布表を参照し、$P(Z \leq -0.5)$の値を確認します。
列は少数第一位を表していて今回は0.50の値を知りたいので、縦が0.5,横が0の値を読み取ります。マイナスの値は載っていませんが正規分布は左右対称なので-をとって0.50の値を読みとればよいです。
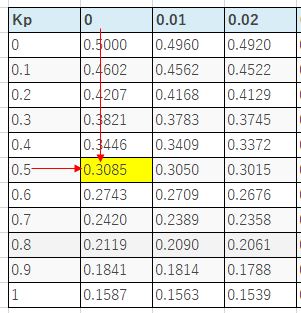
$P(x=<-0.5)=0.3085=30.85%$が答えになります。
問2解答
問2では目標とする平均が大きくなり規格値までの余裕が大きくなります。100mmを切る確率は小さくなりそうだと予想できますね。
ステップ1 変換の式
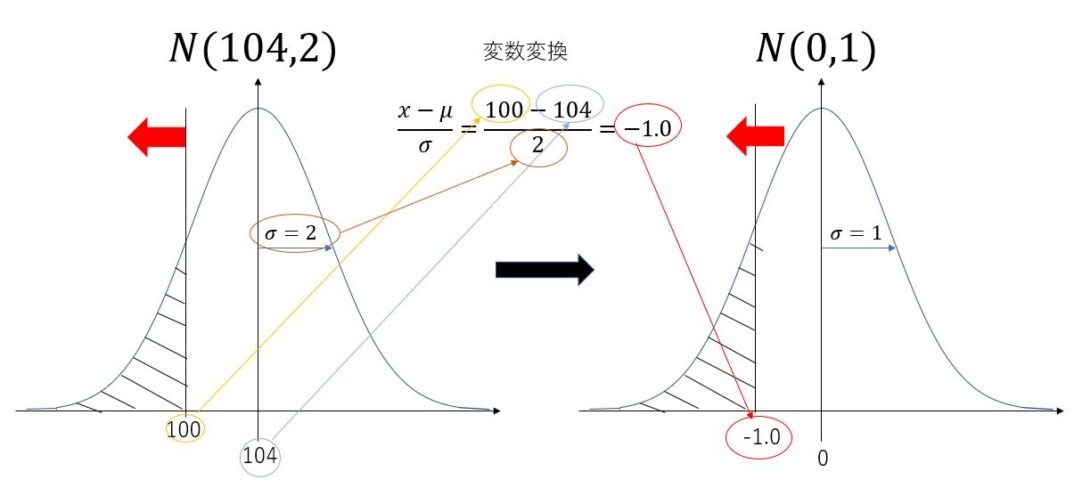
$\frac{x-\mu}{\sigma}=\frac{100-104}{2}=-1.0$
ステップ2 標準正規分布表の読み取り
ステップ1の変数変換で100mm以下は標準正規分布上では-1.0以下と変換されました。
ここで標準正規分布から$Kp=x=<-1.0$となる確率を読み取る。
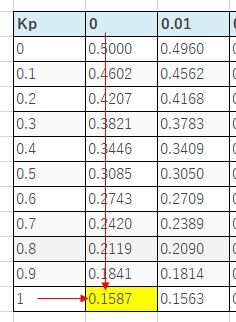
$P(x=<-1.0)=0.1587=15.87%$が答えになります。
問3解答
問3では装置の加工精度が上がりました。正規分布の幅が狭まりシャープになるので製品が規格外になる確率は問1よりも小さくなると予想されます。
ステップ1 変換の式
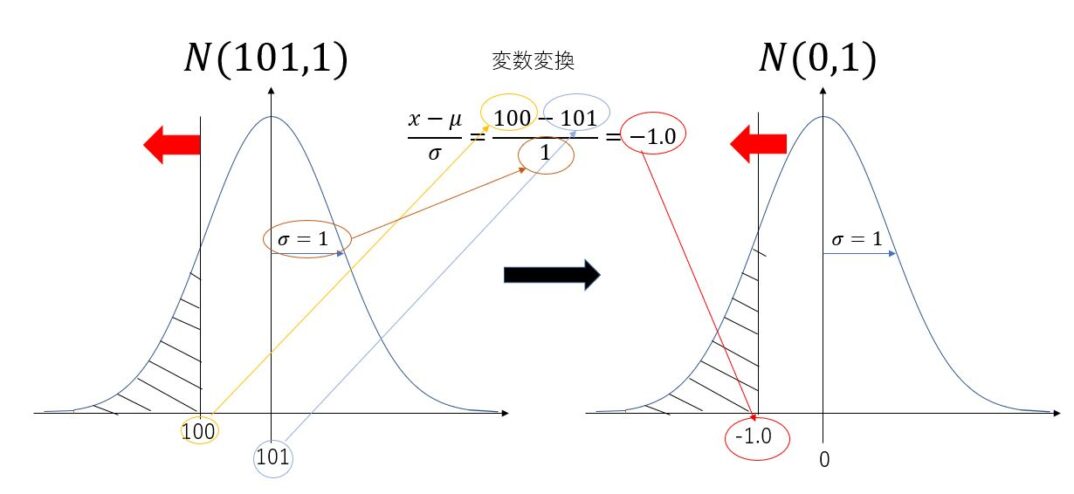
$\frac{x-\mu}{\sigma}=\frac{100-101}{1}=-1.0$
ステップ2 標準正規分布表の読み取り
問2と同じ作業を行います。
$P(x=<-1.0)=0.1587=15.87%$が答えになります。

人の手によらない作業、NC旋盤など工作機械で仕上げた寸法は正規分布に従うといわれています。逆に人の手による作業は一様分布などを仮定することがあります。
まとめ
QC検定2級、3級で頻出の正規分布の問題を取り上げました。
正規分布の計算問題は大まかに3パターンに分けられます。
- 正規分布そのものの特徴
- 標準偏差範囲が占める割合
- ある特性値について規格値以上または以下である確率
一番最後のパターンについては平均を動かして計算するものと標準偏差を狭めて再計算するものと組み合わされることが多いですが、変数変換さえできれば、あとは表の読み取りの問題です。
QC検定2級の計算問題や攻略法についても記事を書いています。





コメント